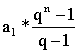Ha egy — 0-t nem tartalmazó — számsorozat minden tagját osztjuk az előtte lévő taggal, és a hányados állandó, akkor a sorozat mértani sorozat.

A hányados jele: q (quotiens — kvóciens: hányados latinul)

(Másképp: Ha a számsorozat hányadossorozata állandó, akkor a sorozat mértani sorozat.)

A mértani sorozat növekvő, ha q > 1 és a₁> 0.

A mértani sorozat csökkenő, ha 0 < q < 1 és a₁> 0.

A mértani sorozat konstans (állandó), ha q = 1.

Ha a mértani sorozat adott tagját megszorozzuk a hányadossal, akkor a rákövetkező, ha az adott tagját elosztjuk a hányadossal, akkor a megelőző tagot kapjuk.

A mértani sorozat tetszőleges, n-edik tagjának, első tagjának és hányadosának kiszámítására használható képlet:

a_n = a₁ * q^(n-1)

A mértani sorozat tetszőleges tagját megkapjuk, ha az első tagot megszorozzuk a hányadosnak a keresett tag sorszámánál 1-gyel kisebb hatványával.

A mértani sorozat első n tagjának összege: S_n

S_n = ha q ¹1

S_n = a₁*n ha q = 1