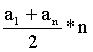Ha a számsorozat bármely tagjából a megelőző tagot kivonva a különbség állandó, akkor a sorozat számtani sorozat.

A különbség jele: d (differencia: különbség latinul)

(Másképp: Ha a számsorozat különbségsorozata állandó, akkor a sorozat számtani sorozat.)

A számtani sorozat növekvő, ha d > 0.

A számtani sorozat csökkenő, ha d < 0.

A számtani sorozat konstans (állandó), ha d = 0.

Ha a számtani sorozat adott tagjához hozzáadjuk a differenciát, akkor a rákövetkező, ha az adott tagjából kivonjuk a differenciát, akkor a megelőző tagot kapjuk.

A számtani sorozat tetszőleges, n-edik tagjának, első tagjának és különbségének kiszámítására használható képlet:

a_n = a₁ + (n – 1) * d

Az első taghoz hozzáadjuk, a különbségnek a keresett tag sorszámánál 1-gyel kevesebbszeresét.

A számtani sorozat első n tagjának összege: S_n

S_n =