|
|
||||
|
|
||||
|
Ábrázoljuk a g: x képlettel megadott
másodfokú függvényt függvénytranszformációval! A
képletből kiderül, hogy másodfokú függvénnyel van dolgunk. Ezért kezdjük az
ábrázolást t az x |
||||
|
A kiindulási
függvényből a műveleti sorrend szabályait figyelembe véve jutunk el az
ábrázolandó függvény képletéhez. |
||||
|
|
||||
|
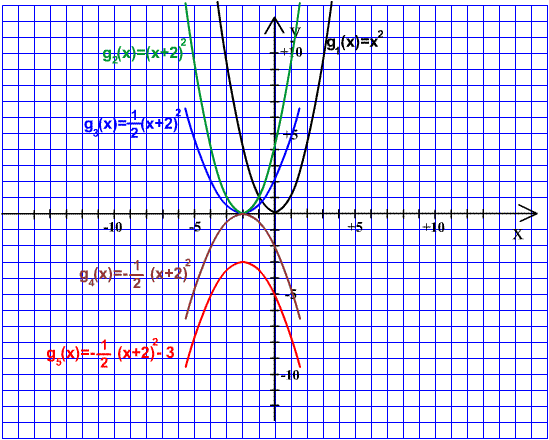
1. függvény |
g1(x) = x2 |
|
||
|
|
|
|
||
|
2. függvény |
g2(x) = (x +2)2 |
Eltolás az x tengely
mentén balra két egységgel |
||
|
|
|
|
||
|
3. függvény |
g3(x) = |
|
||
|
|
|
|
||
|
4. függvény |
g4(x) = – |
Tükrözés az x
tengelyre. |
||
|
|
|
|
||
|
5. függvény |
g(x) =
– |
Eltolás az y tengely
mentén lefelé három egységgel. |
||
|
|
|
|
||
|
A változás mindig a
sorrendben előző függvény grafikonjához képest történik. |
||||
|
|
|
|
||
|
|
||||
|
|
||||
|
A képletet nem kötelező a grafikon mellé
írni, de célszerű olyan színnel írni, vagy aláhúzni, mint amilyennel a
grafikont rajzoltuk. |
||||
|
|
||||