y = f(x)	y = f(x)	y = f(x)
y = |x|	y = x^2	y =
y = a*f(x)	y = a*f(x)	y = a*f(x)
y = a*|x|	y = a*(x )^2	y =
Ha az f(x) képlettel adott függvény függvényértékét a > 1 számmal szorozzuk, akkor az f(x) függvény grafikonját az y tengely irányában a-szorosára nyújtva kapjuk az a*f(x) képlettel adott függvény grafikonját. Ha az f(x) képlettel adott függvény függvényértékét 0 < a < 1 számmal szorozzuk, akkor az f(x) függvény grafikonját az y tengely irányban a-szorosára zsugorítva kapjuk az a*f(x) képlettel adott függvény grafikonját.
Példa
Ábrázoljuk a g: x 2|x| és a h: x |x| képlettel megadott abszolútérték-függvényeket! (A függvényeket két lépésben ábrázoljuk)
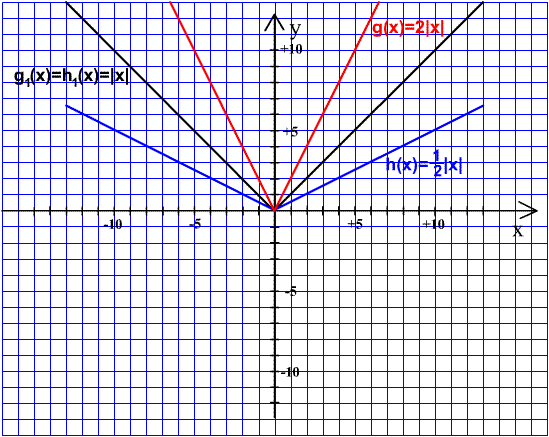
1. függvény: f(x)	g1(x) = |x|	h1(x) =|x|
2. függvény: a* f(x)	g(x) = 2|x|	h(x) = |x|
Az g(x) = 2|x| függvény esetében a =+2, tehát a >1, ezért nyújtással kapjuk az új grafikont. A g1 függvény minden függvényértéke a 2-szeresére változik. A h(x) = |x| függvény esetében a =+, tehát 0< a <1, ezért zsugorítással kapjuk az új grafikont. A h1 függvény minden függvényértéke az -szeresére változik. A V csúcsa a helyén marad, hisz 2-szer 0 és-szer 0 is 0.
Annyi függvényértéknek vesszük a kétszeresét, (felét) amennyi már elegendő a grafikon megrajzolásához. Abszolútérték–függvény esetén elég mindkét száron egy-egy ponthoz tartozó függvényérték kétszeresét (felét) venni.