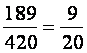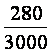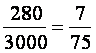|
|
|
TÉTEL: (Állítás): Adott a c
racionális szám. Legyen
A c = – Véges tizedes tört, ha a nevező prímtényezős
alakjában csak 2 vagy 5, illetve 2 és 5 prímtényezők szerepelnek. – Végtelen tiszta szakaszos tizedes tört, ha a
nevező prímtényezői között sem a 2, sem az 5 nem szerepel. A végtelen tiszta
szakaszos tizedes törtben minden tizedes jegy ismétlődik. Pl.: 54,325325325325….. – Végtelen vegyes szakaszos tizedes tört, ha a
nevező prímtényezői között a 2 és/vagy 5-ön kívül más prímszám is szerepel. A
végtelen vegyes szakaszos tizedes törtben nem minden tizedes jegy ismétlődik.
Pl.: 9,571818181818….. |
|
|
|
Példa |
|
|
|
Határozzuk meg az
osztás elvégzése nélkül, hogy a következő racionális számok tizedes tört
alakja véges-, vagy végtelen tizedes tört! |
|
|
|
1.
Hozzuk a törtet a legegyszerűbb alakra!
Írjuk fel a nevező prímtényezős
alakját! 20 = 2 * 2 * 5 A prímtényezős alakjában csak 2 és 5
szerepel, ezért: A |
|
|
|
|
|
2.
Ez a tört nem egyszerűsíthető. Írjuk fel a nevező prímtényezős
alakját! 429 = 3 * 11 * 13 A prímtényezős alakjában sem 2 sem 5 nem szerepel, ezért: A » (0,603729603729…) |
|
|
|
|
|
3.
Hozzuk a törtet a legegyszerűbb alakra!
Írjuk fel a nevező prímtényezős
alakját! 75 = 3 * 5 * 5 A prímtényezős alakjában az 5 mellett
2-től különböző prímszám szerepel, ezért: A » (0,093333333333333….) |
|
|
|
|