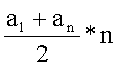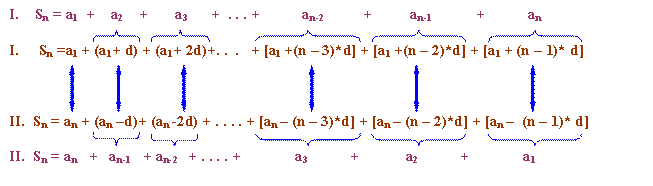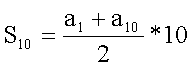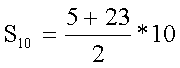|
|
|
|
|
Ha a számsorozat bármely tagjából a megelőző
tagot kivonva a különbség állandó, akkor a sorozat számtani sorozat. A különbség jele: d (differencia:
különbség latinul) (Másképp: Ha a számsorozat
különbségsorozata állandó, akkor a sorozat számtani sorozat.) A számtani sorozat növekvő, ha d > 0. A számtani sorozat csökkenő, ha d < 0. A számtani sorozat konstans (állandó), ha
d = 0. Ha a számtani sorozat adott tagjához
hozzáadjuk a differenciát, akkor a rákövetkező, ha az adott tagjából kivonjuk
a differenciát, akkor a megelőző tagot kapjuk. A számtani
sorozat tetszőleges, n-edik tagjának, első tagjának
és különbségének kiszámítására használható képlet: an = a1
+ (n – 1) * d Az első taghoz
hozzáadjuk, a különbségnek a keresett tag sorszámánál 1-gyel kevesebbszeresét. |
|
Példa |
|
|
|
Határozzuk meg a számtani
sorozat első öt elemét, ha ismerjük a 15. tagot, és a különbséget! a15 =
38 d = 3 a1 = ? a2 = ? a3
=? a4 =
? a5 = ? an = a1 + (n – 1) * d a15 = a1 + (15 – 1) * 3 38 = a1 + (15 – 1) * 3 38 = a1 + 42 //-42 -4 = a1 a1 = -4 a2 = -1 a3 = 2 a4 = 5 a5 = 8 |
|
|
|
A számtani sorozat
első n tagjának összege: Sn Sn = |
|
|
|
Bizonyítás: |
|
|
|
A számtani sorozat
első n tagjának összegét megkapom, ha az elsőtől az n-edikig
valamennyi tagot összeadom. I.
Sn = a1 + a2
+ a3 + a4 +.. . . + an-1 + an-2 + an |
|
|
|
Az összeadandók sorrendjének felcserélhetőségéből következik, hogy a
számtani sorozat első n tagjának összegét úgy is megkapom, ha az n-ediktől, az elsőig valamennyi tagot összeadom. A két
összeg csak a tagok sorrendjében különbözik. II. Sn
= an + an-1 + an-2 + . . . . + a4+ a3 + a2 +
a1 |
|
Minden tag felírható az első
tag és a különbség, és az n-edik tag és a különbség
segítségével is, felhasználva, hogy ha a számtani sorozat adott tagjához
hozzáadjuk a differenciát, akkor a rákövetkező, ha az adott tagjából kivonjuk
a differenciát, akkor a megelőző tagot kapjuk. |
|
|
|
|
|
|
|
I. + II. = 2 Sn A kettős nyíllal összekötött
tagok összege a1 + an. Mivel
n darab ilyen tag van: 2 Sn = (a1 + an
) * n // :2
Pontosan a bizonyítandó állítást kaptuk. |
|
|
|
Példa |
|
|
|
Határozzuk meg a számtani
sorozat első 10 elemének az összegét, ha
a1 = 5 d = 2
Ahhoz, hogy a képletet alkalmazni tudjuk,
szükségünk van a 10. tagra. an = a1 + (n – 1) * d a10 = 5 + (10 – 1) * 2 a10 = 23
S10 = 140 |
|
|