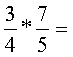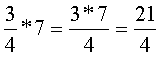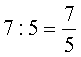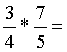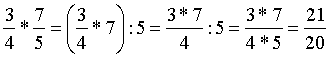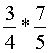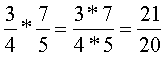|
|
|
Törtet törttel úgy
szorzunk, hogy a számlálót szorozzuk a számlálóval, a nevezőt szorozzuk a
nevezővel. A szorzás jelölése után megpróbálunk egyszerűsíteni. |
|
|
|
|
|
|
|
Használjuk
fel a szorzat változásáról tanultakat!
Szorozzuk meg először az |
|
|
|
a. |
|
|
|
|
|
|
|
Ezt a
szorzást el tudjuk végezni. (Lásd: tört szorzása egész számmal.) |
|
|
|
|
|
Csökkentsük
most a szorzót az ötödére! Osszuk el a szorzót 5-tel! |
|
|
|
|
|
|
|
A
változatlan szorzandót szorozzuk az új szorzóval! |
|
|
|
b. |
|
|
|
|
|
(Eredetileg ennek a szorzatnak keressük az
értékét.) Ha pontosan az egyik szorzótényezőt
valahányad részére csökkentjük, akkor a szorzat is ugyanannyiad
részére csökken. |
|
|
|
Az
a szorzatbeli szorzót ötödére
csökkentettük. Így a szorzat is ötödére csökken. |
|
|
|
|
|
|
|
Tudjuk tehát, hogy a
|
|
|
|
Vegyük
észre, hogy ezt az eredményt kapjuk akkor, ha a számlálót megszorozzuk a
számlálóval, a nevezőt, pedig a nevezővel! |
|
|
|
|
|
|
|
|
|
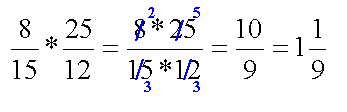
Példa |
|
|
|
|
|
|
|
Egyszerűsítés: A 8-at és a 12-őt néggyel
osztottuk. A 25-öt és a 15-öt öttel. Érdemes még a szorzások elvégzése előtt
egyszerűsíteni, mert így talán csökken a számolási hibák esélye. |